Over the last month I have been doing a few different experiments, with the Raspberry Pi and Mathematica, to develop a number of different lessons/experiments for our students. I don’t have much time  for educational theorists so I take an empirical approach to teaching and believe it is important for teachers to be counted among “those who can do”.

Theory often motivates many changes to the educational system in this country. Consider recent changes to the New Zealand Maths Curriculum, which introduce more emphasis on statistics. The changes seem sensible. Students now gain a better understanding of the statistical process and the variability inherent  in sampling and data.

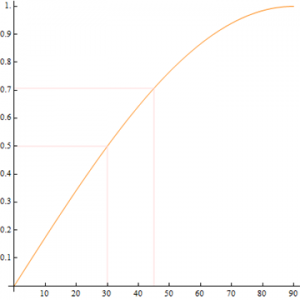
Nevertheless, there are problems with the implementation of this new approach. The usual problems of NCEA , where teachers spoon-feed students and teach directly to the  assessment they deliver, are common. Technically speaking, it seems that students gain the understanding that  Statistics is a narrative activity (a form of story telling). I  am not in favor of the narrative  approach, since many flaws in statistical reasoning are caused by our tendency to tell stories and  join the dots. I encourage my students to withhold judgment, unless there is strong evidence, and to also consider base rates when making  inferences. Story telling seems particularly prevalent when it comes to time series analysis.

Maths and statistics students should develop a maker mentality and that means they need to code. Essentially, code is maths brought to life. While report writing and analysis has it’s place, it is  a bureaucratic activity, while  making  and experimentation leads to new ideas, technology and growth. The thoughts detailed in this video do match my experience when it comes to using maths.

My post,Wi Fi to the Beehive and Raspberry Pi,in the Wolfram Community shows how running a few experiments leads to some interesting new ideas.

This is the CDF version of our Christmas Card.

Mathematica on the Raspberry Pi is very usable for basic mathematical and programming tasks. This is the benchmark report.

Here is a comparison with my desktop which runs very well.

The dimensions  of the Raspberry Pi are 85.60mm x 56mm x 21mm.

A case is a good idea.

I have been using Mathematica for about three years. I have thought about getting my students to use it, and now seems the right time since it is freely available for home use on the Raspberry Pi.

I believe that programming skills are essential if students are going to bring maths to life and solve interesting problems. If you can’t convert mathematical concepts into code, advanced maths skills are of little practical use. The screenshot shows Mathematica code run on the Raspberry Pi.

An expert in an occupation or task, that requires skill, notes regularities and common patterns because they are opportunities for automation. As far as teaching goes certain concepts always seem to be problematic or draw incorrect answers, these regularities make the teachers job easy because they mark areas that need attention and opportunities for growth.

Recently I have been working with a number of physics students on Faraday’s Law. Students need an intuitive understanding of the Sin function because it describes how the magnetic flux changes as a generator rotates. A common misconception that the majority of students hold is that when the angle between the field lines and the coil is 45 degrees the flux will be 50% of the maximum amount, however the actual proportion is 71%. This bias is due to the  way we use shortcuts when reasoning, consequently my physics students memorize the important values of Sin[x].

This year we have ten students learning calculus and at least half of them will study it next year when they go to university. Engineering, economics and architecture are the most common career paths for our calculus students.

I have been teaching calculus since 1997. During this time, I have had a large enough sample of students to make reliable inferences about skill levels and common biases. In fact student errors are extremely predictable and can be quantified statistically. However, the most interesting thing about teaching is designing a sequence of lessons that will develop their understanding.

Recent changes to NCEA Level 2 have weakened basic knowledge of graphs in a number of students studying year 13 calculus.  The graphs assessment is now an internal, students could use technology to investigate more realistic and engaging scenarios, however the current coverage of graphs is narrower and only marginally more constructive than before and some schools have decided not to teach graphs in year 12.  A similar unwelcome development in year 13 calculus is that some schools don’t teach trigonometry, consequently a number of students are not properly prepared for rigorous tertiary courses like engineering.

Currently all our students are studying integration, but over the last month the first five minutes of their lessons has been used to revise basic graphs and their key features. Calculus is visual and these graphs economically encode many mathematical facts.

The following are the graphs we have been revising. The image and the interactive CDF below were prepared using Mathematica.

If you want to try the CDF you will need to download cdf player.

[WolframCDF source=”http://www.ew.org.nz/wp-content/uploads/2013/09/Blog29-09-2013b.cdf” width=”641″ height=”695″ altimage=”http://www.ew.org.nz/wp-content/uploads/2013/09/Blog29-09-2013b.png” ]